Una de las pautas de números más interesantes el es triángulo de Pascal (llamado así en honor de Blaise Pascal, un famoso matemático y filósofo francés).
Para construir el triángulo, empieza con "1" arriba, y pon números debajo formando un triángulo.
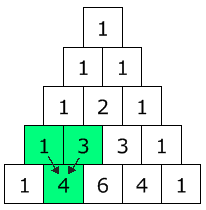
Cada número es la suma de los dos números que tiene encima, menos los extremos, que son siempre "1".
(Aquí está remarcado que 1+3 = 4)
|
 |
| |
|
Pautas en el triángulo
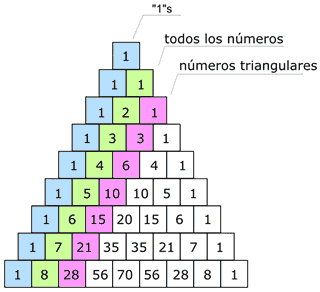 |
Diagonales
La primera diagonal es, claro, sólo "unos", y la siguiente son todos los números consecutivamente (1,2,3, etc.)
La tercera diagonal son los números triangulares
(La cuarta diagonal, que no hemos remarcado, son los números tetraédricos.)
|
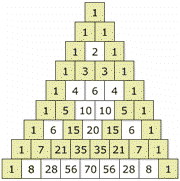
Pares e impares
Si usas distintos colores para los números pares e impares, obtienes un patrón igual al del Triángulo de Sierpinski
|
 |
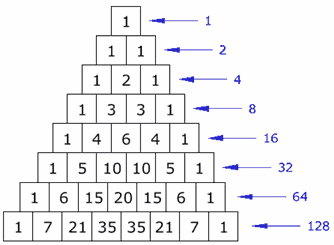 |
Sumas horizontales
¿Notas algo en las sumas horizontales? ¿Hay algún patrón? ¡Es increíble!
Se dobla cada vez (son las potencias de 2).
|
Sucesión de Fibonacci
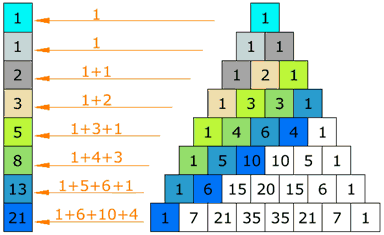
Prueba esto: empieza con un 1 de la izquierda, da un paso
arriba y uno al lado, suma los cuadrados donde caigas (como en el
dibujo)... las sumas que salen son la sucesión de Fibonacci.
(La sucesión de Fibonacci se hace sumando dos números para
conseguir el siguiente, por ejemplo 3+5=8, después 5+8=13, etc.)
|
 |
|
 |
Simetría
El triángulo es simétrico, esto quiere decir que se ve igual desde la derecha que desde la izquierda
|
|
Usar el triángulo de Pascal
Caras y cruces
El triángulo de Pascal te dice cuántas combinaciones de caras y
cruces de pueden salir tirando monedas. Así puedes averiguar la
"probabilidad" de cualquier combinación.
Por ejemplo, si tiras una moneda tres veces, sólo hay una
manera de sacar tres caras (CCC), pero hay tres maneras de sacar dos
caras y una cruz (CCX, CXC, XCC), también tres de sacar una cara y dos
cruces (CXX, XCX, CXX) y sólo una de sacar tres cruces (XXX). Esta es la
pauta "1,3,3,1" en el triángulo de Pascal.
|
Tiradas |
Resultados posibles (agrupados) |
Triángulo de Pascal |
| 1 |
H
T |
1, 1 |
| 2 |
HH
HT TH
TT |
1, 2, 1 |
| 3 |
HHH
HHT, HTH, THH
HTT, THT, TTH
TTT
|
1, 3, 3, 1 |
| 4 |
HHHH
HHHT, HHTH, HTHH, THHH
HHTT, HTHT, HTTH, THHT, THTH, TTHH
HTTT, THTT, TTHT, TTTH
TTTT |
1, 4, 6, 4, 1 |
| |
... etc ... |
|
 |
¿Cuál es la probabilidad de sacar exactamente dos caras con 4 monedas?
Hay 1+4+6+4+1 = 16 (o 4×4=16) resultados posibles, y 6 de
ellos dan exactamente dos caras. Así que la probabilidad es 6/16, o
37.5%
|
Combinaciones
El triángulo también muestra cuántas
combinaciones de objetos son posibles.
Por ejemplo, si tienes 16 bolas de billar, ¿de cuántas maneras
puedes elegir tres de ellas (sin hacer diferencia del orden en que las
eliges)?
Respuesta: baja a la fila 16 (la primera es la fila 0), y mira 3
lugares a la derecha, allí está la respuesta, 560. Aquí tienes un trozo
del triángulo en la fila 16:
1 14 91 364 ...
1 15 105 455 1365 ...
1 16 120 560 1820 4368 ...
Polinomios
El triángulo de Pascal también te da los coeficientes en la expansión de un binomio:
| Potencia |
Expansión polinomial |
Triángulo de Pascal |
| 2 |
(x + 1)2 = 1x2 + 2x + 1 |
1, 2, 1 |
| 3 |
(x + 1)3 = 1x3 + 3x2 + 3x + 1 |
1, 3, 3, 1 |
| 4 |
(x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1 |
1, 4, 6, 4, 1 |
| |
... etc ... |
|
Las 15 primeras líneas
Como referencia, aquí tienes las filas 0 a 14 del triángulo de Pascal
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
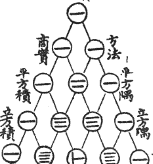 |
Los chinos ya lo conocían
Este dibujo se titula "El antiguo gráfico del método de los siete cuadrados multiplicadores". Ver imagen completa
Esto es de la portada del libro de Chu Shi-Chieh "Ssu Yuan Yü Chien" (Espejo precioso de los cuatro elementos), escrito en 1303 (¡hace más de 700 años!), y en el libro se dice que el triángulo ya era conocido más de dos siglos antes.
|
El quincunce
 |
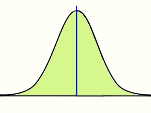
Esta asombrosa máquina creada por Sir Francis Galton es un triángulo de Pascal hecho con palos. Se llama quincunce.
Las bolas se dejan caer sobre el primer palo y rebotan hasta abajo del triángulo donde caen en pequeños contenedores.
| Parece completamente aleatorio (y lo es) pero después de un rato verás que las bolas caen en un bonito patrón: la distribución normal. | | |
 |
|
Fuente: http://www.disfrutalasmatematicas.com/triangulo-pascal.html









