Los griegos tomaron el alfabeto de los fenicios hacia el s. IX a. C., gracias a los contactos comerciales que mantenían con ellos a lo largo de todo el Mediterráneo, especialmente en torno a Chipre o Rodas.
En la actualidad, se le ha dado varios significados a cada una de las letras en diferentes campos:
| código | símbolo | código | símbolo | código | símbolo | código | símbolo | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Alpha |  | Beta | 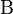 | Gamma | 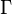 | Delta | 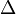 | ||||
| Epsilon |  | Zeta |  | Eta |  | Theta |  | ||||
| Iota |  | Kappa | 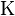 | Lambda | 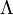 | Mu |  | ||||
| Nu |  | Xi |  | Pi |  | Rho |  | ||||
| Sigma |  | Tau |  | Upsilon |  | Phi | 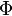 | ||||
| Chi |  | Psi |  | Omega | 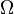 | ||||||
| alpha |  | beta |  | gamma |  | delta | 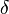 | ||||
| epsilon |  | zeta | 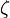 | eta | 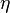 | theta |  | ||||
| iota |  | kappa |  | lambda | 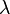 | mu |  | ||||
| nu | 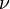 | xi | 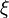 | pi |  | rho |  | ||||
| sigma | 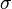 | tau | 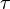 | upsilon |  | phi |  | ||||
| chi |  | psi | 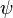 | omega |  |
Si quieres hacer una prueba de cuanto sabes sobre las letras griegas haz click aquí
Algunas letras griegas usadas en la matemática:
- ( ) La constante de Euler-Mascheroni
) La constante de Euler-Mascheroni
 ) La constante de Euler-Mascheroni
) La constante de Euler-Mascheroni 
- (λ) La longitud de onda

- (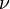 ) El coeficiente de Poisson
) El coeficiente de Poisson
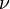 ) El coeficiente de Poisson
) El coeficiente de Poisson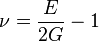
- (π) El número, si quieres saber mas, click aqui
π = 3.1415926535897932384...
- (ρ) El radio en sistema de coordenadas polares

- (Σ) Sumatorias

- (σ) Desviación estándar - parámetro estadístico

- - (φ) La Función Fi de Euler

- (Φ) El número áureo o de oro Fi (Φ,φ)

- (χ) La distribución ji -cuadrado (χ²)
